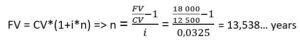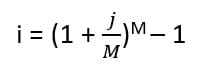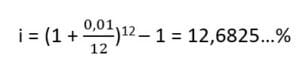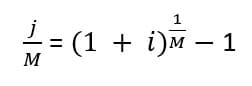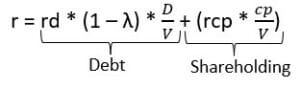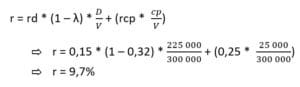Everyone has heard the famous expression: “Time is money”. Indeed, when we stop there, we exchange our time for money every day.
One can work for a company, manufacture products in order to sell them, build an e-commerce business, sell one’s services, etc. In short, we exchange or transform our time in order to make money.
However, are there other relationships between time and money?
Time and money are linked by a principle of exchange and by interest. First, we exchange our time in order to obtain a monetary contribution, whether by receiving a salary or by selling a product or service. Second, money and time are linked by interest rates which have a direct impact on the value of money over time.
This article aims to familiarize the reader with the principles of equivalence. This makes it possible to compare payments (or series of payments) by finding their equivalence over time.
Mastering this aspect is necessary since it corresponds to one of the pillars of the profitability analysis!
In the next sections of the text, simple interest, compound interest and the cost of capital (for project management) will be detailed. These topics are related to time and money mathematically.
Examples will be presented and a Calculator is available to properly assess the (monetary) value of Your future projects (time)!
Free Time Money Calculator
Time-Money Relationship: Simple Interest
In the context where the interest earned accumulates only on the capital initially invested, we speak of simple interest. The interest is therefore not capitalized.
In other words, the interest received does not accumulate interest in turn.
When we talk about simple interest, we find several variables that relate the interest rate to time and money. Here is the list of variables used to calculate the present and future values of an investment or expense:
CV: Current value of an amount of money at time 0
FV: Future value of amount after capitalizing interest
i: Interest rate per time period
n: Number of periods of investment or loan
I: Amount of interest earned or paid
Now, mathematically, we can relate money and time according to the prevailing interest rate for our project. Here are the mathematical formulas related to simple interest:
I = i * CV * n
FV = CV*(1+i*n)
Example of using a Simple Interest Rate
A private investor lends you $10,000 to carry out renovations in your facilities. The loan is for a period of 5 years and the simple interest rate is 15% per year. What is the future value of this loan? How much money will you have to pay in interest?
FV = CV * (1+i*n) = $10,000 * (1 + 0.15 * 5) = $17,500
I = i * CV * n = 0.15 * $10,000 * 5 = $7500
You will therefore have to repay $17,500 over 5 years and the loan will cost you a total of $7,500 in interest.
Here is a final example that shows how to use simple interest rate formulas to determine how long it takes for an investment to reach the desired amount.
You have a project in mind and it costs $18,000. Currently, you hold $12,500 in a 3.25% annual simple interest account. How long should you wait under these conditions before reaching your goal?
The formulas presented in the article are pre-programmed in an Excel File in order to save you time! It’s Free, don’t hesitate to download it!
Time-Money Relationship: Compound Interest
In an investment context, compound interest is much more attractive. Conversely, for a payment, it is much less advantageous than a simple rate. Especially if the investment or loan horizon is long!
To put this into perspective, Albert Einstein said, “Compound interest is the eighth wonder of the world. He who understands it is enriched; whoever does not understand it, pays for it. »
So what should we understand from this “marvel”?
Interest is said to be compounded when interest earned over time in turn produces interest earnings. That is to say that at each end of period (n), the interest earned accumulates to the capital of the beginning of the period (n-1) to generate interest during the following period (n+1 ).
On the other hand, if we are talking about a loan, then the interest that must be paid to the lender is added to the capital to be repaid and in turn, generates interest to be paid. A little less advantageous for the payer, let’s say. We therefore better understand the quote from Einstein!
Now, how do you calculate the effect of compound interest?
Free Time Money Calculator
Compound Interest: Mathematical Relationship
For compound interest, we find the same variables as with simple interest, but the mathematical formulas differ.
Again, an Excel spreadsheet already contains all the formulas for you! If you are curious, here is how we calculate the effect of compound interest over time for an investment (we wish you 😉) or a payment (☹).
Future Value of Capital:
FV = CV*(1 + i) n
Present Value (of an amount to be received in the future):
CV = FV*(1 + i)-n
Example of using a Compound Interest Rate
Let’s take the example of the private investor and simple interest rates. This time, the lender gives you a loan of $10,000 over 5 years, but the interest rate of 15% is compounded. What will be the difference between the total amounts of the simple VS compound rate?
With a simple rate, you had to repay $17,500 to the lender, or $7,500 in interest.
With a compound rate, we get:
FV = CV*(1 + i) n = $10,000*(1 + 0.15) 5 = $20,113.57
The amount of interest to be paid therefore goes from $7,500 to $10,113.57! That’s over $2600 more.
However, in an investment context, we see that compound interest rates are really wonderful! And this, especially since the investment horizon is long.
We must therefore take advantage of this relationship between money and time as quickly as possible to maximize our income and add this constraint when calculating project profitability to ensure that our projects are really profitable!
Consult our article on Project Profitability for more information!
Before moving on to the next section, let’s look at one last example.
It’s your lucky day and you win a Winner for Life lottery. You, therefore, have the choice between an immediate sum of $350,000 OR $1,000 for life for 20 years. Knowing that you could derive an average annual compound return of 6%. What would be the smartest option?
First, $1000 * 20 years * 52 week/year = $1,040,000
Next,
FV = CV*(1 + i) n = FV = $350,000*(1 + 0.6) 20 = $1,122,497.42
This example should be taken with a grain of salt for several reasons. So before you get carried away, here they are:
- The future value of the $350,000 invested at 6% interest is about $100,000 greater than the $1,000 per week. However, this is considering that the entire $350,000 is invested, while the $1,000 per week is not (0).
- If we take the 6% and look at how much money per year we could get from the $350,000, then we get $21,000, or the equivalent of $403 in interest per week. Less than $1000.
- The $350,000 makes it possible to obtain large financing quickly for large-scale projects that could yield much more than 6%.
Let us now move on to the next section on the principle of equivalence.
Principle of Equivalence
Whether we are talking about a company or an individual, the terms of payment do not matter (generally) provided that a discount factor makes the options equivalent.
To illustrate this, consider the following example:
Here are three payment options to repay a $40,000 loan over 4 years at a rate of 5%.
This example is inspired by the profitability analysis course at UQTR. The course was set up with the collaboration of several teachers. (UQTR, 2018).
At first glance, there does not seem to be any equivalence between the 3 options since the amounts to be paid are different. However, if we look at the side of the lender, it retains at all times its 5% return on capital granted. Here is the proof:
| Options | Sum of capital outstanding at the end of each year | Total interest paid | Ratio |
|---|---|---|---|
| 1 | 60 000 | 3 000 | 0,05 |
| 2 | 90 000 | 4 500 | 0,05 |
| 3 | 94 575 | 4728,75 | 0,05 |
Ratio = Total interest paid / Sum of principal outstanding at the end of each year
Option 1, 2, and 3 are therefore equivalent from the point of view of the lender who receives 5% interest on the loaned capital. This principle of equivalence “forms the basis of cost-benefit analysis since it allows payments or series of payments to be compared by finding their equivalence at a given point in time. (UQTR, 2018)
Free Time Money Calculator
Nominal, effective, and periodic interest rates – Conversion
Interest rates are generally expressed on an annual basis. However, in many cases, capitalization is not done annually. For example, the interest on a loan could be capitalized (added to the principal) every month.
In addition, the frequency of capitalization varies the return obtained on the capital. The higher the frequency, the higher the efficiency.
Nominal Interest Rate:
The nominal interest rate is the rate that is calculated annually. However, the capitalization frequency may differ. It must therefore be indicated in the terms of the loan or investment. The nominal rate is represented by “j”.
Consider the following example, a monthly rate of 1% would be represented by a nominal rate j = 12% compounded monthly.
Effective Interest Rate:
The effective interest rate is the actual rate obtained or paid over a period of one year. This takes into account the frequency of capitalization. In the case where the frequency is higher than once a year, the nominal rate is greater than the effective rate.
Conversely, if the capitalization frequency is more than one year, then the effective rate is lower than the nominal interest rate.
It is therefore the interest rate that interests us since it represents the “true” rate obtained on the capital invested or paid on borrowed capital.
Periodic Interest Rate:
A periodic interest rate represents an interest rate compounded over “M” period. There are periodic interest rates monthly (denoted “m”), half-yearly (“s”), quarterly (“t”), etc.
Conversion of Effective, Nominal, and Periodic Interest Rates
To convert one interest rate to another, there are a few mathematical formulas to achieve this. Formulas are presented and an Excel file is available to calculate conversions quickly and simply.
Periodic Rate –> Effective Rate
Example :
Let’s take a monthly rate of 1%. What is the effective rate?
Effective Rate –> Periodic Rate
Periodic Rate –> Nominal Rate
Cost of capital
When analyzing the profitability of a project, one must take into account the relationship between time and money. The longer the project is spread over time, the more relevant it becomes to discount or calculate the future value of an investment.
As a result, income and payments are indexed using an interest rate in order to compare them on the same time basis. In general, this rate is called the minimum acceptable rate of return (TRAM).
When analyzing the profitability of a project, the TRAM is compared with the rate to finance the project. Obviously, the TRAM must be higher than the financing rate of the project for it to be profitable.
In addition, the minimum acceptable rate of return for a project must be higher than the rate the company (or individual) could obtain by placing its money in a financial institution. Indeed, why bother to make a project if it pays more to leave your money in the bank? (UQTR, 2018)
For the capital cost calculation, the following are relevant terms and their definitions:
- r = Cost of capital
- rd = Borrowing rate (bank or credit union)
- λ = Tax rate
- D = Loan amount
- V = Company market value
- cp = Outstanding shares
- rcp = Equity (involving promoter risk) or promoter rate of return
There are two components in the calculation of the cost of capital. Debt and Shareholding. THE mathematical formula for calculating the cost of capital is:
Example :
A project manager for a furniture company wants to acquire a new machine to increase its production capacity. To do this, he must borrow $225,000 at a rate of 15% from the bank to finance his project.
The current tax rate for this company is 32%, the market value is $300,000 and there are 25,000 shares outstanding. Eventually, the promoters’ rate of return was set at 25%.
What is the capital cost for such a project?
The capital cost of this project is therefore 9.7%
Free Time Money Calculator
Conclusion:
In conclusion, the relationship between time and money is explained by two principles. The exchange of our time in order to do an activity that brings in money or through the interest that causes the value of money to fluctuate over time.
In this article, the concept of simple and compound interest has been explained in order to illustrate the mathematical relationship between time and money.
In addition, the different rates (effective, nominal, and periodic) have been explained. The conversion from one rate to another has also been illustrated using mathematical formulas. An Excel file is however available to speed up the various calculations presented in the article!
Finally, the importance between time and money was shown in the calculation of project profitability. The calculation of the capital cost and the analysis of the MRR (minimum acceptable rate of return) was therefore presented.
Reference:
Profitability Analysis Course, UQTR, 2018. Chapitre 2 : Intérêt et relations argent-temps.