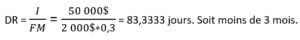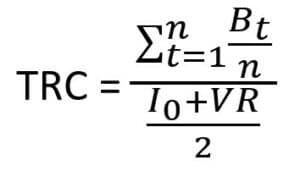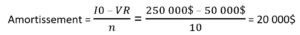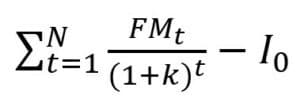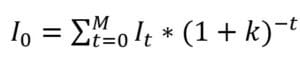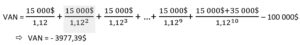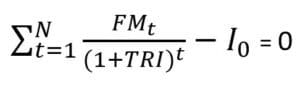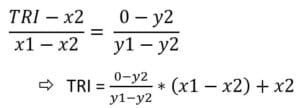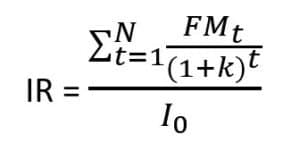L’analyse de rentabilité permet d’assurer la profitabilité des projets entrepris. Du moins, elle permet de réduire les risques de pertent!
L’un des nos articles portant sur la relation entre le temps et l’argent a pour but de familiariser le lecteur aux principes d’équivalence.
Cela permet de comparer des paiements (ou série de paiements) en trouvant leur équivalence dans le temps.
La maitrise de cet aspect est nécessaire puisqu’elle correspond à l’un des piliers de l’analyse de rentabilité!
Dans cet article, on se penche maintenant sur l’analyse de rentabilité et les méthodes de calculs pour la réaliser.
La source de ces informations provient du cours d’analyse de rentabilité de projet de l’Université du Québec à Trois-Rivières en collaboration avec plusieurs professeurs (PHD) et chargé de cours (M.SC. A OU MBA).
Qu’est-ce que l’Analyse de Rentabilité de Projet?
Lorsqu’on analyse la rentabilité d’un projet, on cherche à garantir que celui-ci nous rapportera plus d’argent qu’il nous en a coûté pour le réaliser.
De plus, on souhaite obtenir un rendement supérieur à celui qu’on aurait pu facilement obtenir à la banque (ou la caisse) si on avait placé cet argent.
Idéalement, on cherchera à obtenir un rendement qui reflète l’effort (monétaire, physique et psychologique) que l’on a déployé dans notre investissement!
L’analyse de rentabilité de projets consiste à déterminer le seuil de rentabilité minimum d’un investissement. C’est-à-dire le point où la somme des dépenses moins la somme des gains est égale à 0 ou à l’objectif de rentabilité visé.
Encore une fois, on veut obtenir un rendement qui est représentatif de l’effort que l’on met dans un projet.
Par exemple, s’il faut débourser 100 000$ et 350 heures de travail pour obtenir un rendement de 5%, alors qu’on peut aisément obtenir 3% à la banque en ne faisant rien, alors pourquoi mettre autant d’effort?
L’analyse de rentabilité est un outil qui permet d’évaluer le rendement d’un projet en plus de fournir des informations indispensables à la prise de décision.
Principe de Base de l’Analyse de Rentabilité
Avant de poursuivre avec les techniques et les calculs d’analyse de rentabilité, voici quelques notions de base pertinentes à l’évaluation de projets d’investissement. Ces notions sont tirées de (UQTR, 2018).
- L’analyse de rentabilité d’un projet doit uniquement tenir compte des coûts et des gains supplémentaires apportés par le projet à l’étude.
- Il est important d’utiliser les taux d’intérêt pertinents pour comparer des montants d’argent disponible à des dates différentes. D’autant plus que certains projets peuvent s’étaler sur plusieurs années. Les taux utilisés pour effectuer l’analyse sont souvent ceux que l’on peut obtenir facilement et sans risque.
- Les flux monétaires correspondent à des entrées et des sorties d’argent « effectives ». Contrairement aux notions comptables, ils ne réfèrent pas à des revenues et des dépenses.
- Il faut ajouter les frais supplémentaires tels que les frais de démarrage et la constitution d’un fonds de roulement supplémentaire aux sorties de fonds dit « directe » (achat d’équipement, frais d’installation, terrain, etc.). Dans le même ordre d’idée, il faut déduire les entrées d’argent telles que les subventions gouvernementales, crédit d’impôt, etc.
Analyse de rentabilité : Méthode de calculs
Dans certains cas, il suffit de jeter un coup d’œil aux entrées et aux sorties d’argent pour avoir une bonne idée de la rentabilité d’un projet. Toutefois, lors de projet complexe, cette façon de faire peut rapidement devenir nébuleuse.
Dans cet article, sans passer à travers toutes les méthodes d’analyses, les plus importantes sont expliquées. Voici un tableau qui présente ces méthodes d’analyse de la rentabilité de projets.
|
Méthode d’Analyse de Rentabilité |
Description |
Acronyme |
| Délai de récupération | Détermine la période de temps nécessaire à la récupération du capital investi au début du projet. |
DR |
|
Taux de rendement comptable |
Mesure le « rapport entre le bénéfice annuel moyen [net] et l’investissement comptable moyen pendant le projet. » | TRC |
| Valeur actuelle nette | « Mesure la différence entre les flux monétaires positifs actualisés et la valeur actuelle des montants investis. » |
VAN |
| Taux de rendement interne | Taux de rentabilité correspondant au taux d’intérêt pour lequel la VAN est de 0. |
TRI |
|
Indice de rentabilité |
Rapport entre les entrées et les sorties d’argent (flux monétaire « positif » et « négatif »). | IR |
| Taux de rendement interne intégré | Taux de rentabilité correspondant au taux d’intérêt pour lequel la VAN est de 0. Toutefois, cette technique (contrairement à la VAN, au TRI et à l’IR) n’assume pas que les flux monétaires soient réinvestis à taux unique. |
TRI* |
(UQTR, 2018)
Délai de récupération (DR)
Le délai de récupération, ou la période de recouvrement, représente le temps minimum nécessaire pour récupérer le capital investit dans un projet.
Règle générale, si un projet se rentabilise en 1 an ou moins, alors on va de l’avant. Toutefois, dans des projets de plus grande envergure, on pourrait aller bien au-delà d’une année.
Pour calculer le DR, voici la formule mathématique, ainsi que les variables utilisées dans l’équation :
DR = I / FM
où I représente le capital investit et FM le flux monétaire du projet par période de temps (semaine, mois, année ou autre).
Exemple :
L’ingénieur d’une entreprise réalise une cartographie de chaîne de valeur et cible le goulot de l’usine.
En investissant 50 000$ pour acquérir une nouvelle machine plus récente et plus rapide, il estime que l’entreprise pourrait produire 2000$ de production supplémentaire par jour.
De plus, les marges de l’entreprise sont de 30%.
Quelle serait le délai de récupération d’un tel projet?
Taux de rendement comptable (TRC)
La méthode du taux de rendement comptable est basée sur les « bénéfices comptables plutôt que sur les flux monétaire ». Cette méthode calcule le « rapport entre le bénéfice annuel moyen après impôt et l’investissement comptable moyen pendant le projet. » (UQTR, 2018).
Pour calculer le TRC, voici les variables à connaître pour comprendre l’équation mathématique :
- TRC = Taux de rendement comptable
- Bt = Bénéfice après impôt de l’année « t »
- n = Durée de vie du projet
- I0 = Investissement initial
- VR = Valeur résiduelle
Maintenant que l’on connaît les variables, voici la formule du TRC :
Exemple :
Une entreprise pense investir 250 000$ pour acquérir une nouvelle machine. La durée de vie de la machine et sa valeur résiduelle sont respectivement de 10 ans et 50 000$.
En investissant dans cette machine, l’entreprise espère obtenir les bénéfices avant impôt présenté dans le tableau ci-dessous. Le taux d’imposition est de 35% et le taux de rendement minimum exigé par la haute direction est de 15%.
L’entreprise devrait-elle aller de l’avant avec acquisition?
| Année | Bénéfices avant amortissement et impôt | Amortissement | Bénéfices avant impôt | Bénéfices nets |
| 1 | 75 000$ | 20 000$1 | 55 000$2 | 35 750$3 |
| 2 | 75 000$ | 20 000$ | 55 000$ | 35 750$ |
| 3 | 75 000$ | 20 000$ | 55 000$ | 35 750$ |
| 4 | 60 000$ | 20 000$ | 40 000$ | 26 000$ |
| 5 | 60 000$ | 20 000$ | 40 000$ | 26 000$ |
| 6 | 60 000$ | 20 000$ | 40 000$ | 26 000$ |
| 7 | 50 000$ | 20 000$ | 30 000$ | 19 500$ |
| 8 | 40 000$ | 20 000$ | 20 000$ | 13 000$ |
| 9 | 30 000$ | 20 000$ | 10 000$ | 6 500$ |
| 10 | 25 000$ | 20 000$ | 5 000$ | 3 250$ |
| Total | 550 000$ | 200 000$ | 120 000$ | 227 500$ |
1. Calcul de l’amortissement :
2. Bénéfice avant impôt :
Bénéfice avant impôt = Bénéfice avant amortissement et impôt – Amortissement
Bénéfice avant impôt = 75 000$ – 20 000$ = 55 000$
3. Bénéfice après impôt :
Bénéfice après impôt = Bénéfice avant impôt * (1 – i) où i représente le taux d’imposition.
Bénéfice après impôt = 55 000$ * (1 – 0,35) = 35 750$
Calcul du Taux de Rendement Comptable :
TRC = 15,16% ≥ 15%, donc l’entreprise devrait procéder à l’investissement puisqu’il respecte le taux minimum requis.
Il faut toutefois noter que la méthode du taux de rendement comptable comporte ses risques puisqu’elle se base sur les chiffres comptables plutôt que sur les flux monétaires.
Valeur actuelle nette (VAN)
La méthode de la VAN calcule la différence entre les entrées d’argents (flux monétaires positifs) actualisés et la valeur actuelle du capital investi.
Dans ce calcul, un taux d’actualisation « pertinent est établi selon le niveau de risque du projet et il correspond au taux de rendement exigé. »
Un taux sans risque peut être utilisé dans une « situation de certitude. ». (UQTR, 2018).
Dans le calcul de VAN, les variables sont les suivantes :
- FMt = Flux monétaire net à la période t
- N = Durée total du projet
- k = Taux d’actualisation pertinent
- I0 = Investissement initital
- It = Investissement à la période t
- M = Temps nécessaire pour effectuer les déboursés
La formule mathématique de la valeur actuelle nette est la suivante :
Dans un contexte où l’investissement initial s’étale sur plusieurs périodes, alors on obtient l’expression suivante pour I0 :
Maintenant, passons à un exemple pour concrétiser la section sur la VAN.
Exemple :
L’entreprise manufacturière Steel Inc. désire investir dans une nouvelle machine de découpe laser pour augmenter sa productivité. Après quelque recherche, l’entreprise s’intéresse à un modèle au coût de 100 000$.
Selon leur estimation, cette machine permettrait d’augmenter leur profit de 15 000$/année pour les 10 prochaines années.
Dans 10 ans, l’entreprise pense pouvoir revendre cette machine pour environ 35 000$. Si l’entreprise utilise un taux de rendement acceptable minimum de 12%, devrait-elle investir dans cette machine ou poursuivre ses recherches?
Les gestionnaires de l’entreprise Steel Inc. feraient mieux de poursuivre leur recherche puisque celui-ci ne répond pas au taux de rendement minimum acceptable de l’entreprise. Pour ce faire, il manquerait près de 4 000$ à gagner.
Si la VAN est égale à 0, alors cela veut dire que l’on respecte le taux de rendement minimum. Il va de soi qu’il faut donc utiliser son jugement, surtout dans l’optique où les calcules se font avec des estimations. Toutefois, il faut chercher à mettre les chances de son côté.
Taux de rendement interne (TRI)
Le taux de rendement interne (TRI), ou encore le taux de rentabilité, d’un projet correspond au taux où la VAN = 0. Dans le cas où l’on dépasse ce taux, on considère qu’un projet n’est pas rentable ou ne répond pas au critère de rentabilité de l’entreprise (effort-impact).
Pour isoler le TRI, on utilise la formule suivante :
De cette formule, il n’est pas évident d’isoler le taux de rendement interne puisque la relation entre le TRI et la VAN n’est pas linéaire.
De ce fait, il est recommandé d’y aller par tâtonnement dans un premier lieux afin de trouver des valeurs positives et négatives de la VAN.
Par la suite, on interpole les résultats pour isoler le TRI.
Interpolation linéaire
| TRI | VAN |
| x1 | y1 |
| TRI | 0 |
| x2 | y2 |
Formule :
Pour augmenter la précision des résultats, il est recommandé de trouver des valeurs qui ne dépasse pas 5% d’écart (entre y1 et y2).
Pour mieux conceptualiser cette méthode, procédons à un exemple!
Exemple :
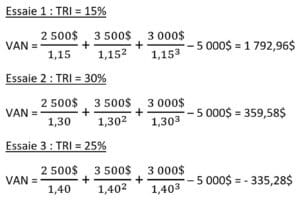
Une petite entreprise d’entretien ménager songe acquérir un robot aspirateur industriel pour réduire ses coûts de main d’œuvre et augmenter sa productivité. Un tel robot coûte 5 000$ et l’entreprise estime économiser les montants montrés dans le tableau des flux monétaires ci-dessous.
Flux monétaire annuels du projet de robot aspirateur
| Année | Flux monétaire (FMt) |
| 0 | -5 000$ |
| 1 | 2 500$ |
| 2 | 3 500$ |
| 3 | 3 000$ |
Maintenant, pour isoler le TRI, il faut réaliser quelques essais de calculs pour trouver une valeur positive et négative dans la VAN avec un écart maximal de 5%.
Note : Avec Excel, il est très rapide d’effectuer ces essaies erreurs.
Interpolation linéaire :
| TRI | VAN |
| 40% | -335,28$ |
| TRI | 0 |
| 30% | 359,58$ |
Maintenant, il ne suffit que d’interpoler pour obtenir le taux de rendement interne de ce projet.
Le TRI de ce projet est donc de 35,17% ce qui est excellent. L’entreprise devrait donc aller de l’avant avec ce projet.
Note : En allant avec des données plus précises, on obtient un TRI d’environ 34,88%. Plus les données sont près de 0, plus la précision est grande.
Indice de rentabilité (IR)
L’indice de rentabilité est une méthode qui calcule le rapport entre les flux monétaires positifs et négatifs d’un projet. Pour considérer un projet rentable, l’indice de rentabilité doit être supérieur à 1.
Pour mesurer l’IR, on utilise la formule suivante :
Exemple :
Reprenons l’exemple effectuer avec la VAN. Si l’entreprise Steel Inc. avait utilisé la méthode de l’indice de rentabilité, quelle aurait-été leur conclusion face à leur projet ?
L’indice de rentabilité est inférieur à 1, donc l’entreprise en vient à la même conclusion qu’avec la méthode de la valeur actuelle nette. Elle rejette le projet puisque celui-ci n’atteint pas le rendement minimum exigé par l’entreprise, soit 12%.
Taux de rendement interne intégré* (TRI*)
Finalement, la dernière méthode présentée dans cet article est l’analyse du taux de rendement interne intégré.
Les méthodes de calculs de la VAN, du TRI et de l’IR sont plus précise que les deux premières méthodes (DR et TRC) présentés puisqu’elles prennent en considération la valeur de l’argent dans le temps (relation temps-argent).
Cependant, la valeur actuelle nette, le taux de rendement interne et l’indice de rentabilité « assument que les flux monétaires sont réinvestis à un taux unique ». (UQTR, 2018).
Avec la méthode du taux de rendement interne intégré, on suppose un « taux de réinvestissement » raisonnable et soutenable dans le futur afin de recalculer le taux de rendement d’un projet.
Cela permet donc de diminuer le risque de certains projets et d’assurer la rentabilité de ceux-ci. Puisqu’il n’y a pas de certitude en investissement, cette méthode permet de valider la rentabilité de projet avec des taux de réinvestissement du capital plus conservateur.
Cette méthode se fait en deux étapes. Celles-ci seront présenté sous-forme d’exemple. Les formules seront présentées par la même occasion.
Exemple :
Reprenons l’exemple de l’entreprise d’entretien ménager réaliser dans la section sur le taux de rendement interne. Le TRI obtenu était de l’ordre de 35%. Recalculons le taux de rendement, mais cette fois-ci, avec un taux de réinvestissement de 8%. Ce qui semble plus raisonnable pour l’entreprise.
| Année | Flux monétaire (FMt) |
| 0 | -5 000$ |
| 1 | 2 500$ |
| 2 | 3 500$ |
| 3 | 3 000$ |
Étape 1 :
Calculer la valeur future des flux monétaires positif avec un taux de réinvestissement de 8%
VF = 2 500$ * (1+0,08)2 + 3 500$ * (1+0,08)1 + 3000 * (1+0,08)0
⇒ VF = 2 916$ + 3 780$ + 3 000$
⇒ VF = 9696$
Étape 2 :
Comparer la valeur future avec l’investissement initial pour isoler le taux de rendement interne intégré.
Le taux de rendement passe de 35,17% à 24,66% avec un taux de réinvestissement de 8% (versus 12% initialement). Avec un rendement espéré comme celui-ci, l’entreprise peut aller de l’avant avec le projet, et ce sans soucis puisqu’elle est confiante de pouvoir maintenir un taux de réinvestissement de 8%.
Conclusion :
En conclusion, il existe plusieurs méthodes pour calculer la rentabilité d’un projet. Dans cet article, sans être exhaustif, les méthodes les plus populaires ont été expliqués et illustrées à l’aide d’exemple.
Parmi les méthodes présentées, les méthodes de la valeur actuelle nette (VAN), du taux de rendement interne (TRI) et de l’indice de rentabilité (IR) sont considéré comme plus précises, car elle considère la relation entre le temps et l’argent. N’hésitez pas à consulter notre article à ce sujet!
Finalement, la méthode du taux de rendement interne intégré (TRI*) a été expliqué. Cette méthode permet de réduire le risque des projets en calculant le taux de rendement interne avec un taux de réinvestissement plus faible que le TRI. Cela permet d’assurer la rentabilité d’un projet en utilisant un taux de réinvestissement que l’entreprise est confiante de réaliser à travers les années.
Référence :
UQTR, 2018. Analyse de Rentabilité – Chapitre 3, PDF.