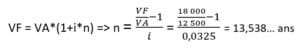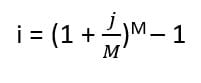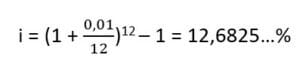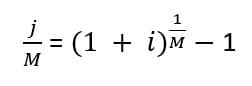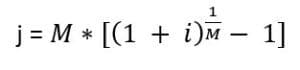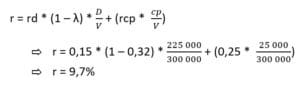Tout le monde à déjà entendu la fameuse expression : « Le temps, c’est de l’argent ». Effectivement, quand on s’y arrête, on échange notre temps pour de l’argent à tous les jours.
On peut travailler pour une entreprise, fabriquer des produits dans le but de les vendre, construire une entreprise de e-commerce, vendre ses services, etc. Bref, on échange ou transforme notre temps dans le but de faire de l’argent.
Toutefois, existe-t-il d’autres relations entre le temps et l’argent ?
Le temps et l’argent sont reliés par un principe d’échange et par les intérêts. Dans un premier temps, on échange notre temps dans le but d’obtenir une contribution monétaire que ce soit en recevant un salaire ou en vendant un produit ou un service. Dans un deuxième temps, l’argent et le temps sont reliés par les taux d’intérêts qui ont un impact direct sur la valeur de l’argent au fils du temps.
Cet article a pour but de familiariser le lecteur aux principes d’équivalence. Cela permet de comparer des paiements (ou série de paiements) en trouvant leur équivalence dans le temps.
La maitrise de cet aspect est nécessaire puisqu’elle correspond à l’un des piliers de l’analyse de rentabilité!
Dans les prochaines sections du texte, les intérêts simples, composés et le coût du capital (pour la gestion de projet) seront détaillées. Ces sujets relient le temps et l’argent de façon mathématique.
Des exemples seront présentés et un Calculateur est disponible afin de bien évaluer la valeur (monétaire) de Vos futurs projets (temps)!
Relation temps argent
Relaton Temps-Argent : Intérêt Simple
Dans le contexte où l’intérêt gagné se cumule uniquement sur le capital investi au départ, on parle d’intérêt simple. L’intérêt n’est donc pas capitalisé.
En d’autres mots, les intérêts perçus ne cumulent pas d’intérêt à leur tour.
Lorsqu’on parle d’intérêt simple, on retrouve plusieurs variables permettant de mettre en relation le taux d’intérêt, le temps et l’argent. Voici la liste des variables permettant de calculer les valeurs actuelles et futures d’un investissement ou d’une dépense :
VA : Valeur actuelle d’un montant d’argent au temps 0
VF : Valeur future du montant après avoir capitalisé les intérêts
i : Taux d’intérêt par période de temps
n : Nombre de période du placement ou de l’emprunt
I : Montant d’intérêt gagné ou payé
Maintenant, de façon mathématique, on peut relier l’argent et le temps en fonction du taux d’intérêt en vigueur pour notre projet. Voici les formules mathématiques en lien avec l’intérêt simple :
I = i * VA * n
VF = VA*(1+i*n)
Exemple de l’utilisation d’un Taux d’Intérêt Simple
Un investisseur privé vous prête un montant de 10 000$ pour effectuer des rénovations dans vos installations. Le prêt est d’une durée de 5 ans et le taux d’intérêt simple est de 15% par année. Quelle est la valeur future de ce prêt ? Combien d’argent devrez vous payer en intérêt?
VF = VA * (1+i*n) = 10 000$ * (1 + 0,15 * 5) = 17 500 $
I = i * VA * n = 0,15 * 10 000$ * 5 = 7500$
Vous devrez donc rembourser 17 500$ sur 5 ans et le prêt vous coutera un total de 7 500$ en intérêt.
Voici un dernier exemple qui montre comment utiliser les formules de taux d’intérêt simple dans le but de déterminer le temps nécessaire à un placement pour atteindre un montant désiré.
Vous avez un projet en tête et celui-ci en coute 18 000$. Actuellement, vous détenez 12 500$ dans un compte à intérêt simple de 3,25% annuel. Combien de temps devriez-vous attendre dans ces conditions avant d’atteindre votre objectif ?
Les formules présentées dans l’article sont préprogrammées dans un Fichier Excel dans le but de vous faire économiser du temps! C’est Gratuit, n’hésitez pas à le télécharger!
Relaton Temps-Argent : Intérêt Composé
Dans un contexte de placement, les intérêts composés sont beaucoup plus intéressants. À l’inverse, pour un paiement, c’est beaucoup moins avantageux qu’un taux simple. D’autant plus si l’horizon de placement ou de prêt est longue!
Pour mettre cela en perspective, Albert Einstein disait que : « les intérêts composés sont la huitième merveille du monde. Celui qui le comprend s’enrichit ; celui qui ne le comprend pas, le paie. »
Alors qu’est-ce que l’on doit comprendre de cette « merveille »?
L’intérêt est dit composé lorsque les intérêts gagnés au fil du temps produisent à leur tour des gains en intérêt. C’est-à-dire qu’à chaque fin de période (n), l’intérêt gagné s’accumule au capital du début de la période (n-1) pour générer des intérêts lors de la période suivante (n+1).
D’un autre côté, si l’on parle d’un prêt, alors les intérêts que l’on doit verser au prêteur s’additionne au capital à rembourser et génère à leur tour des intérêts à payer. Un peu moins avantageux pour le payeur disons. On comprend donc mieux la citation d’Einstein!
Maintenant, comment calculer l’effet des intérêts composés?
Relation temps argent
Intérêt Composé : Relation Mathématique
Pour les intérêts composés, on retrouve les mêmes variables qu’avec les intérêts simples, mais les formules mathématiques diffèrent.
Encore une fois, un chiffrier Excel contient déjà toutes les formules pour vous! Si vous êtes curieux, voici comment on calcul l’effet des intérêts composés en fonction du temps pour un placement (on vous le souhaite 😉) ou un paiement (☹).
Valeur Future du Capital :
VF = VA*(1 + i) n
Valeur Actuelle (d’un montant à recevoir dans le futur) :
VA = VF*(1 + i)-n
Exemple de l’utilisation d’un Taux d’Intérêt Composé
Reprenons l’exemple avec l’investisseur privé et les taux d’intérêts simple. Cette fois-ci, le prêteur vous fait un prêt de 10 000$ sur 5 ans, mais le taux d’intérêt de 15% est composé. Quelle sera la différence entre les montants totaux du taux simple VS composé?
Avec un taux simple, vous deviez remboursé 17 500$ au prêteur soit 7 500$ d’intérêt.
Avec un taux composé, on obtient :
VF = VA*(1 + i) n = 10 000$*(1 + 0,15) 5 = 20 113,57$
Le montant d’intérêt à payé passe donc de 7 500$ à 10 113,57$! Soit plus de 2600$ de plus.
Toutefois, dans un contexte de placement, on voit que les taux d’intérêts composés sont vraiment merveilleux! Et ce, d’autant plus que l’horizon de placement est long.
Il faut donc profiter le plus rapidement possible de cette relation entre l’argent et le temps pour maximiser ses revenues et ajouter cette contrainte lors de calcul de rentabilité de projet afin de s’assurer que nos projets soit réellement rentable!
Consulter notre article sur la Rentabilité de projet pour plus d’information!
Avant de passer à la prochaine section, regardons un dernier exemple.
C’est votre jour de chance et vous gagner une loterie du type Gagnant à vie. Vous avez donc le choix entre une somme immédiate de 350 000$ OU 1 000$ à vie pendant 20 ans. Sachant que vous pourriez tiré un rendement annuel moyen composé de 6%. Quelle serait l’option la plus judicieuse?
Premièrement, 1000$ * 20 ans * 52 semaine/année = 1 040 000$
Ensuite,
VF = VA*(1 + i) n = VF = 350 000$*(1 + 0,6) 20 = 1 122 497,42$
Il faut prendre cet exemple avec un grain de sel pour plusieurs raisons. Alors avant de vous emporter, les voici :
- La valeur future du 350 000$ placé à 6% d’intérêt est plus grande d’environ 100 000$ que le 1000$ par semaine. Toutefois, c’est en considérant que la totalité du 350 000$ est placé, alors que le 1000$ par semaine ne l’est pas (0).
- Si l’on prend le 6% et que l’on regarde combien d’argent par année on pourrait tiré du 350 000$, alors on obtient 21 000$, soit l’équivalent de 403$ d’intérêt par semaine. Moins que le 1000$.
- Le 350 000$ permet d’obtenir un grand financement et rapidement pour des projets d’envergure qui pourrait rapport beaucoup plus que 6%.
Passons maintenant à la prochaine section portant sur le principe d’équivalence.
Principe d’Équivalence
Qu’on parle d’une entreprise ou d’un individu, les modalités de paiements importent peu (généralement) à condition qu’un facteur d’actualisation rend les options équivalentes.
Pour illustrer ces propos, prenons l’exemple suivant :
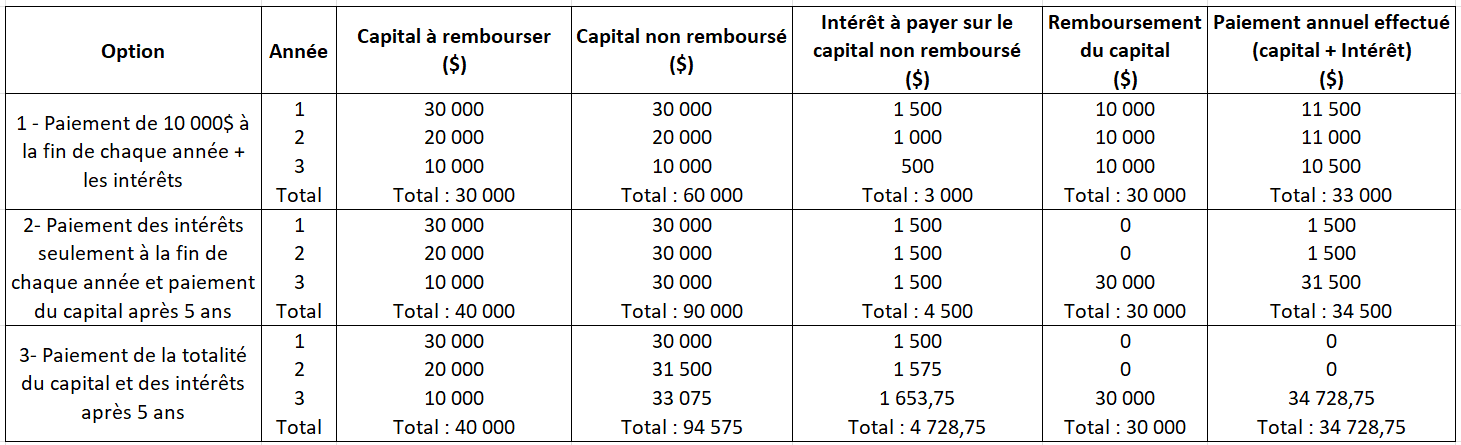
Voici trois options de paiement pour rembourser un prêt de 40 000$ sur 4 ans à un taux de 5%.
Cet exemple est inspiré du cours d’analyse de rentabilité de l’UQTR. Le cours a été monté avec la collaboration de plusieurs professeurs. (UQTR, 2018).
À première vue, il ne semble pas y avoir d’équivalence entre les 3 options puisque les montants à payer sont différent. Pourtant, si l’on regarde du côté du prêteur, celui-ci conserve en tout temps sont 5% de rendement sur capital octroyé. En voici la preuve :
| Options | Somme du capital non remboursé à la fin de chaque année | Total des intérêts déboursés | Rapport |
|---|---|---|---|
| 1 | 60 000 | 3 000 | 0,05 |
| 2 | 90 000 | 4 500 | 0,05 |
| 3 | 94 575 | 4728,75 | 0,05 |
Rapport = Total des intérêts déboursés / Somme du capital non remboursé à la fin de chaque année
L’option 1, 2 et 3 est donc équivalente du point du vue du prêteur qui perçoit 5% d’intérêt sur le capital prêté. Ce principe d’équivalence « constitue la base de l’analyse de rentabilité puisqu’il permet de comparer des paiements ou des séries de paiements en trouvant leur équivalence en un point donnée dans le temps. » (UQTR, 2018)
Relation temps argent
Taux d’intérêt nominal, effectif et périodique – Conversion
Les taux d’intérêts sont généralement exprimés de façon annuel. Par contre, dans plusieurs cas, la capitalisation ne se fait pas annuellement. Par exemple, l’intérêt sur un prêt pourrait être capitalisé (ajouté au capital) à tous les mois.
De plus, la fréquence de capitalisation fait varier le rendement obtenu sur le capital. Plus la fréquence est grande, plus le rendement est élevé.
Taux d’Intérêt Nominal :
Le taux d’intérêt nominal est le taux qui est calculé annuellement. Toutefois, la fréquence de capitalisation peut différer. Il faut donc l’indiquer dans les termes du prêt ou du placement. Le taux nominal est représenté par « j ».
Prenons l’exemple suivant, un taux mensuel de 1% serait représenté par un taux nominal j = 12% capitalisé mensuellement.
Taux d’Intérêt Effectif :
Le taux d’intérêt effectif est le taux réel obtenu ou payé sur un période d’un an. Celui-ci prend en compte la fréquence de capitalisation. Dans le cas où la fréquence est plus élevée qu’une fois par année, le taux nominal est plus grand que le taux effectif.
À l’inverse, si la fréquence de capitalisation est de plus qu’une année, alors le taux effectif est moins élevé que le taux d’intérêt nominal.
C’est donc le taux d’intérêt qui nous intéresse puisqu’il représente le « vrai » taux obtenu sur le capital investi ou payé sur du capital emprunté.
Taux d’Intérêt Périodique :
Un taux d’intérêt périodique représente un taux d’intérêt capitalisé sur « M » période. On retrouve des taux d’intérêts périodiques mensuel (noté « m »), semestriel (« s »), trimestriel (« t »), etc.
Conversion des Taux d’Intérêts Effectifs, Nominaux et Périodiques
Pour convertir un taux d’intérêt vers un autre, il existe quelques formules mathématiques pour y arriver. Les formules sont présentées et un fichier Excel est disponible pour calculer rapidement et simplement les conversions.
Taux Périodique –> Taux Effectif
Exemple :
Prenons un taux mensuel de 1%. Quelle est le taux effectif?
Taux Effectif –> Taux Périodique
Taux Périodique –> Taux Nominal
Relation temps argent
Coût du capital
Lorsque l’on analyse la rentabilité d’un projet, on doit prendre en compte la relation entre le temps et l’argent. Plus le projet s’étale dans le temps, plus il devient pertinent d’actualiser ou de calculer la valeur future d’un investissement.
De ce fait, on indexe les revenues et les paiements à l’aide d’un taux d’intérêt afin de les comparer sur une même base de temps. De façon générale, on nomme ce taux le taux de rendement minimum acceptable (TRAM).
Lors de l’analyse de rentabilité d’un projet, on compare le TRAM avec le taux pour financer le projet. Évidemment, le TRAM doit être supérieur au taux de financement du projet pour que celui-ci soit rentable.
De plus, le taux de rendement minimum acceptable d’un projet doit être supérieur au taux que l’entreprise (ou l’individu) pourrait obtenir en plaçant son argent dans une institution financière. En effet, pourquoi se donner du mal à faire un projet si c’est plus payant de laisser son argent à la banque? (UQTR, 2018)
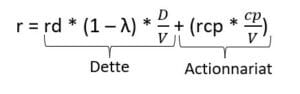
Pour le calcul du coût en capital, voici les termes pertinents, ainsi que leurs définitions :
- r = Coût du capital
- rd = Taux d’emprunt (banque ou caisse)
- λ = Taux d’imposition
- D = Montant de l’emprunt
- V = Valeur marchande de l’entreprise
- cp = Actions en circulation
- rcp = Capitaux propre (impliquant risque des promoteurs) ou taux de rendement des promoteurs
On retrouve deux composantes dans le calcul du coût du capital. La dette et l’actionnariat. LA formule mathématique pour calculer le coût du capital est la suivante :
Exemple :
Un chargé de projet pour une entreprise de meuble désire acquérir une nouvelle machine pour augmenter sa capacité de production. Pour ce faire, il doit emprunter 225 000$ à un taux de 15% à la banque pour financer son projet.
Le taux d’imposition en vigueur pour cette entreprise est de 32%, la valeur marchande de de 300 000$ et on retrouve 25 000 actions en circulation. Finalement, le taux de rendement des promoteurs a été établie à 25%.
Quel est le coût en capital pour un tel projet ?
Le coût en capital de ce projet est donc de 9,7%
Conclusion :
En conclusion, la relation entre le temps et l’argent s’explique par deux principes. L’échange de notre temps dans le but de faire une activité qui rapporte de l’argent ou encore par les intérêts qui font fluctuer la valeur de l’argent dans le temps.
Dans cet article, la notion d’intérêts simple et composé a été expliquer dans le but d’illustrer la relation mathématique entre le temps et l’argent.
De plus, les différents taux (effectif, nominal et périodique) ont été expliqués. La conversion d’un taux à un autre a aussi été illustré à l’aide de formules mathématique. Un fichier Excel est toutefois disponible pour accélérer les différents calculs présentés dans l’article!
Finalement, l’important entre le temps et l’argent a été montré dans le calcul de la rentabilité de projet. Le calcul du coût en capital et l’analyse du TRAM (taux de rendement minimum acceptable) a donc été présenté.
Relation temps argent
Référence :
Cours d’analyse de rentabilité, UQTR, 2018. Chapitre 2 : Intérêt et relations argent-temps.