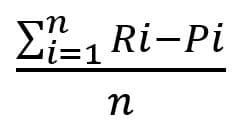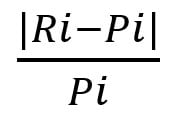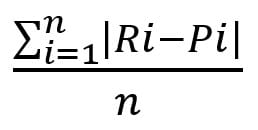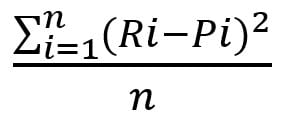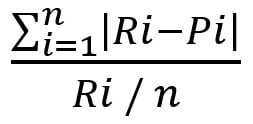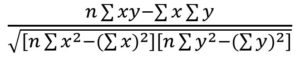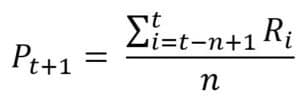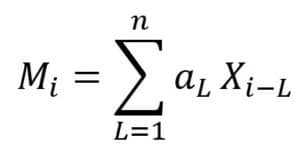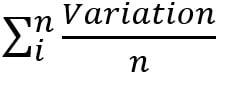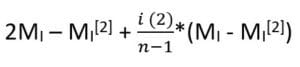Prévisions de Ventes Excel : Guide Complet et Outil Gratuit!

 

Comme vous, nous avons fait nos recherches pour trouver de l’information et des outils sur les prévisions de ventes. Nous n’avons rien trouvé de significatif,  alors on a décidé de conconcter cet article au meilleurs de nos connnaisscances et de notre expertise.

Par la même occasion, on vous propose un outil gratuit pour effectuer vos prévisions!

Les prévisions de ventes permettent de prévoir les ventes futurs d’une entreprise. Avec la bonne méthode et dépendant de la variabilité de l’entreprise, certains modèles peuvent atteindre une précision de l’ordre de 90 à 95%! Ce n’est toutefois par toujours le cas, mais ça reste généralement plus précis que de le faire sur le coin d’une table.

Lors de notre passage dans une PME qui fabrique des cablages à remorques, nous avons développé un outil similaire à celui offert dans l’article. La précisions de l’outil était si bonne (+- 92% en moyenne) que la comptable de l’entreprise l’a conservé pour continuer de s’en servir.

Les prévisions de ventes ont plusieurs utilités qui sont explorés au travers de l’article. Par exemple, l’établissement de budget, l’optimisation de la gestion des stocks, etc.

 

 

Qu’est-ce que les Prévisions de Vente?

 

Les prévisions de vente ont pour but d’estimer les ventes futures d’une entreprise, en dollars ou en unité, dans le but de :

 

• Planifier la stratégie globale de l’entreprise
• Optimiser la répartition des ressources internes
• Déterminer les besoins de liquidités de l’entreprise
• Déterminer quand accroître la capacité de production
• Optimiser la gestion des stocks
• Améliorer la planification et l’ordonnancement de la production

 

De façon plus générale, on pourrait définir la prévision de vente comme une « fonction permettant d’estimer la demande future qu’on établit soit mathématiquement (données historiques), soit intuitivement (connaissance du marché), soit les deux. » (Drolet, Robitaille & Désilets, 2016).

Il existe différent logiciel permettant de calculer et d’estimer les prévisions de ventes d’une entreprise. On peut aussi utiliser Excel et programmer les différents modèles de prévisions pour obtenir de très bon résultat sans avoir à débourser 1 sou!

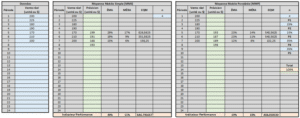
Dans ce texte, un fichier Excel avec les méthodes prévisionnelles les plus populaires est offert aux lecteurs! Chacune des méthodes est présentée et le fichier est expliqué pour faciliter son utilisation. Les indicateurs de performances des méthodes prévisionnels sont aussi présentés et se retrouvent dans l’outil proposé. Voici un exemple de ce fichier complètement gratuit!

 

 

 

Prévision de Ventes et Horizon Temporel

 

Long terme :

Les prévisions à long terme ont un horizon de 2 à 5 ans. Elles sont utilisées dans la planification stratégique de l’entreprise.

L’analyse de ce type de prévision permet, entre autres, de planifier des agrandissements d’usine, l’augmentation de la capacité de production, l’achat de nouveaux équipements ou technologies, les besoins de personnels, etc.

À l’inverse, cela peut permettre d’établir des stratégies de redressement dans le cas où les ventes sont à la baisse.

 

Moyen terme :

À moyen terme, les prévisions de ventes sont établies sur 1 à 2 ans. Cette fois-ci, le but de leur analyse est de déterminer le « budget de fonctionnement de l’entreprise et certaines dépenses du budget d’immobilisation ».

 

Court terme :

Finalement, les prévisions à court terme sont réalisées sur 1 an et moins. Elles ont besoin d’être précises et servent à réaliser la planification des activités de production, l’ordonnancement, la gestion des stocks, etc.

L’analyse des prévisions à court terme est essentielle pour évaluer et optimiser les opérations d’une entreprise. Cela peut permettre de réaliser des économies importantes. Toutefois, une mauvaise analyse peut aussi mener à des pertes importantes d’où l’importance de la précision des données.

 

Une bonne analyse et un bon modèle de prévision permettent de réduire les coûts de stockage, de manutention, de logistique, etc.

 

Défis des Prévisions de Ventes

 

Il existe différentes raisons qui font en sorte qu’il est difficile de prévoir avec exactitude la demande future d’une entreprise. Les principales raisons sont :

• Nouveaux produits sur le marché
• Retrait d’un produit existant
• Promotions des concurrents
• Variation des prix (matière première, énergie, etc.)
• Contexte économique
• Nouvelles technologies

 

Ces défis peuvent faire varier les ventes de l’entreprise et rendre les modèles de prévisions moins précis. Cela fait en sorte que l’on peut surestimer ou sous-estimer la demande future.

Dans le cas où l’on surestime la demande, on risque de sous-utiliser notre personnel et stocker beaucoup de produit. Cela aura pour conséquence d’augmenter les coûts de stockage et de monopoliser des liquidités en stocks qui « dort » sur le plancher.

À l’inverse, en sous-estimant la demande du marché, on risque de devoir recourir au surtemps à la sous-traitance (et donc augmenter le coût de production unitaire), de manquer de stocks (matière première) et de livrer en retard chez les clients (pertes de confiance avec le client).

 

 

 

Rôle des Prévisions de Ventes dans la Budgétisation de l’Entreprise

 

La budgétisation d’une entreprise joue un rôle fondamental dans sa capacité à maintenir une saine gestion de sa trésorerie.

Avant même de se lancer dans les concepts de budgétisation, il est essentiel de comprendre la nuance entre la rentabilité et la liquidité.

La rentabilité est la capacité qu’a l’entreprise à faire des profits. En faisant la somme de tous les revenus et en soustrayant cette somme par l’ensemble des dépenses, on obtient le profit (aussi appelé bénéfice net) d’une entreprise pour la période étudiée. Lorsque les gestionnaires évaluent un projet, ils s’assurent que le projet sera rentable. Néanmoins, le projet a bien beau être potentiellement rentable, mais l’entreprise doit aussi être en mesure de soutenir financièrement ce projet. C’est là qu’entre en jeu la gestion de la liquidité.

La liquidité de l’entreprise doit être évaluée régulièrement. Les gestionnaires doivent s’assurer d’avoir des fonds suffisants pour respecter leurs obligations. Des exemples d’obligations sont le paiement d’un prêt contracté avec une institution financière, le paiement des fournisseurs à temps, le paiement d’un crédit-bail, le paiement des salaires des employés, le paiement des sous-traitants, etc. En d’autres mots, la gestion des liquidités se résume par le fait d’être en mesure de faire un paiement, et ce, au moment convenu.

Ceci étant dit, la budgétisation d’une entreprise traite de la gestion des liquidités.

 

Qu’est-ce qu’un Budget d’Entreprise?

 

Budgétiser permet de prévoir qu’elles seront les entrées et sorties de fonds à venir. Ainsi, les gestionnaires savent s’ils seront en mesure de faire leurs paiements à temps. Dans le contexte où les gestionnaires remarquent qu’il y aura un manque de liquidité à un moment précis, ils devront trouver des sources de financement externe. En d’autres mots, ils devront palier se manque en empruntant, en investissant leurs fonds personnels, en trouvant d’autres investisseurs, en retardant leurs paiements, etc. Généralement, les entreprises ont une marge de crédit déjà autorisée qui permet de pallier les déficits, mais celle-ci est limitée.

Le but de la budgétisation est de prévoir les entrées et sorties de fonds le plus précisément possible. Évidemment, la variabilité des prévisions mène les gestionnaires à prendre des décisions erronées. Il est donc essentiel de s’assurer que la source des prévisions soit valide, sans quoi, l’ensemble de la budgétisation de l’entreprise est biaisé.

La source de l’ensemble de la budgétisation de l’entreprise est les prévisions des ventes.

 

Importance des Prévisions pour le Budget d’Entreprise

 

Vous avez probablement déjà entendu l’expression « Garbage in, Garbage out ». L’intrant principal de la budgétisation est la prévision des revenus. Lorsque les ventes sont prévues, cette prévision agit comme point de départ pour établir le budget des ventes.

Il s’agit du premier budget à réaliser parmi un ensemble de budgets appelé budget directeur. L’objectif derrière la réalisation du budget directeur est de prévoir l’ensemble des entrées et sorties de fonds. Ceci permettra de réaliser le budget de caisse.

Le budget de caisse est le sommaire qui permet à l’entreprise de voir quelles périodes d’une année seront en surplus ou en déficit de liquidité. Ce budget est ensuite utilisé pour établir les états financiers prévisionnels de l’entreprise.

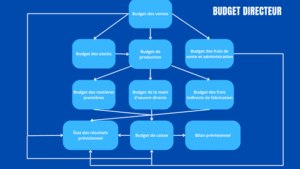
Pour comprendre les liens entre l’ensemble des budgets faisant partie du budget directeur, voici une image montrant le budget directeur d’une entreprise de fabrication :

 

*Image adaptée de l’ouvrage de Garrison, R. Libby, T., & Webb, A. (2016). «Fondements de la comptabilité de gestion», Chenelière Éducation.

 

À noter que les autres types d’entreprises (qui ne sont pas des entreprises de fabrication) regroupent les mêmes budgets que présentés dans l’image ci-dessus, mis à part ceux relatifs à la fabrication. Le tableau suivant montre l’ensemble des budgets par type d’entreprise :

 

Entreprise de fabrication	Entreprise commerciale	Toutes les entreprises
Budget de production	Budget des stocks	Budget des ventes
Budget des matières premières	Budget d’achat de marchandises	Budget des frais de vente et administration
Budget de main-d’œuvre directe		Budget de caisse
Budget des frais indirects de fabrication
Budget des stocks

 

En résumé, sachant que les prévisions des ventes ont un impact majeur sur l’ensemble de la budgétisation de l’entreprise, il est donc crucial d’y accorder un degré d’importance élevé.

D’autant plus, lorsqu’on sait que l’un des plus importants problèmes financiers des entreprises est l’insuffisance de liquidités, on doit redoubler d’ardeur et maîtriser la gestion des liquidités!

Maintenant, comment prévoir efficacement les ventes futures? Les prochaines sections traitent des méthodes prévisionnelles et de l’utilisation du fichier Excel gratuit pour prévoir ses ventes.

 

Quelles sont les Méthodes Prévisionnelles?

 

On retrouve trois types de méthodes prévisionnelles en fonction du contexte de vente de l’entreprise : stable, avec tendance ou saisonnier.

 

 

Les méthodes, présentées dans ce texte, pour les entreprises qui sont stables, c’est-à-dire que leurs ventes suivent un niveau ou une moyenne sont :

 

• Prévisions Naïves
• Moyennes Arithmétiques Simples
• Moyennes Mobiles Simples*
• Moyennes pondérées*
• Lissage Exponentiel Simple*

*Méthodes disponibles et automatisées dans le fichier Excel!

 

Pour ce qui est des entreprises qui sont en croissance, ou qui suivent une tendance, les méthodes présentées sont :

• Régression Linéaire Simple*
• Régression Linéaire Multiple*
• Analyse de la tendance (Variation Moyennes)*
• Moyenne Mobile Double*
• Lissage Exponentiel Simple avec composante de tendance*
• Lissage Exponentiel Double*

 

Finalement, pour les entreprises avec de la saisonnalité, les méthodes sont :

• Prévision à l’aide d’indice saisonnier (+régression linéaire)*
• Méthode par Désaisonnalisation
• Méthode de Winters

 

Méthodes Prévisionnelles et Indicateur de Performance

 

Avant de poursuivre avec les méthodes prévisionnelles plus en détail, voici les principaux indicateurs de performance afin d’évaluer la précision des outils.

Dans le fichier Excel, les indicateurs servent à déterminer en un coup d’œil quelle méthode est la plus adaptée (précise) pour vous!

Les différents indicateurs sont :

 

• L’Erreur ou Écart
• Le Biais ou Erreur Moyenne
• L’Erreur Relative Absolue (ERA)
• L’Erreur Moyen Absolue (ÉMA)*
• L’Erreur Quadratique Moyenne (EQM)*
• La Moyenne des Erreurs Relatives Absolues (MÉRA)*
• Coefficient de Corrélation (R)*
• Coefficient de Détermination (R²)*

*Indicateur utilisé dans le chiffrier Excel.

 

Erreur ou Écart

L’erreur ou l’écart (Ei) est la différence entre les ventes réelles R(i) et la prévision de vente P(i) pour une période (i).

E(i) = R(i) – P(i)

 

Biais ou Erreur Moyenne

 

Le biais ou l’erreur moyenne représente la moyenne des erreurs (écarts) observées après un nombre de périodes n.

L’erreur moyenne indique si une méthode a tendance à donner des prévisions supérieures ou inférieures à la moyenne.

 

Biais =

 

Erreur Relative Absolue (ÉRA)

 

L’erreur relative absolue représente l’erreur sous forme de pourcentage. L’ÉRA donner une indication quant à la précision d’une méthode ou établir un intervalle de confiance pour l’établissement d’une prévision.

Précision : ÉRA(i) = 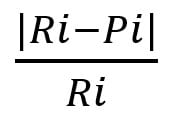 / Intervalle de confiance : ÉRA(i) =

Où Ri : Vente réelle pour la période i, Pi : Prévision de la demande i et i : Indice de période

 

Écart Moyen Absolue (ÉMA)

L’écart absolu moyen « considère l’importance plutôt que le sens de l’erreur de prévision. Un ÉMA faible indique que la méthode utilisée aide à prévoir très bien la demande. » (Drolet, Robitaille & Désilets, 2016)

 

ÉMA =

 

Erreur Quadratique Moyenne (EQM)

 

L’écart quadratique moyen met chacune des erreurs de prévision aux carrées. De la sorte, l’EQM indique si un modèle fournit plus souvent que les autres des écarts de prévisions importants.

 

EQM =

 

Moyenne des Erreurs Relatives Absolues (MÉRA)

 

La moyenne des erreurs relatives absolues est un bon indicateur de performance pour les méthodes. Elle permet de déterminer si un modèle de prévision est précis ou non.

 

MÉRA =

 

 Coefficient de Corrélation (R)

 

Le coefficient de corrélation (R) « indique le degré de relation entre une variable dépendante et une variable indépendante. » (Drolet, Robitaille & Désilets, 2016)

Plus R se rapproche de 1 (ou -1) plus la relation est forte.

 

(-1 ≤ R ≤ 1)

R =

 

R =	Signification
0,90 à 1,00 OU -0.90 à -1,00	Très Bonne Corrélation
0,70 à 0,8999 OU -0,7 à -0,8999	Bonne Corrélation
0,40 à 0,6999 OU -0,4 à -0,6999	Corrélation Faible à Moyenne
-0,3999 à 0,3999	Corrélation Mauvaise ou Inexistante

 

Coefficient de Détermination (R²) 

 

Le coefficient de détermination (R²) « correspond au pourcentage de la variation de la variable dépendante expliqué par la variable indépendante ». (Drolet, Robitaille & Désilets, 2016)

Plus le coefficient de détermination est près de 1, plus on peut prédire avec exactitude la valeur de la variable dépendante (y) selon la valeur de la variable indépendante (x).

En d’autres mots, le modèle mathématique reliant x et y est exact lorsque R² = 1. On utilise cette méthode pour déterminer la précision de modèle utilisant des régressions linéaires ou multiples.

Pour finir, prenons l’exemple suivant. On obtient un coefficient de détermination R² = 0,9. Cela indique que 90% de la variation de la variable Y est expliqué par la variation de la variable X. Le 10% restant varie selon d’autres variables inconnues du modèle mathématique.

 

 

Méthodes Prévisionnelles Sans Tendance Ni Saisonnalité – Prévision des Ventes

 

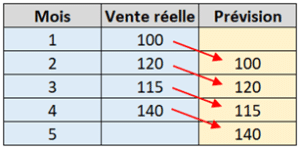
Prévision Naïves

 

La méthode des prévisions naïves est très simple, peu coûteuse, mais peu précise. Pour ces raisons, nous avons décidé de ne pas l’inclure dans le fichier Gratuit.

Cette méthode consiste à utiliser la vente réelle de la période i-1 comme prévision de la période i.

 

Exemple :

 

 

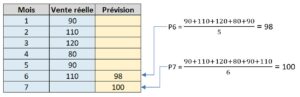
Moyennes Arithmétiques Simples

 

Pour cette méthode, on utilise la moyenne des ventes réelles passées pour déterminer la prévision de la période suivante. C’est une méthode peu coûteuse, simple, mais peu précise « dans un contexte où la demande est dynamique. » Cette méthode nécessite de conserver un certain nombre de données.

Cette méthode n’est pas non plus disponible dans le fichier Excel, puisque la précision est souvent faible.

Il est possible d’utilise cette méthode pour des demandes saisonnières. Dans ce cas, on utilise la moyenne des périodes des « saisons » passées. Par exemple, pour Juin 2022, on utilise la moyenne des ventes de Juin 2018, 2019, 2020 et 2021.

 

Exemple :

 

 

Moyenne Mobile Simple (MMS)

 

La méthode de la moyenne mobile simple est la première de l’article qui est disponible dans le calculateur de prévision de vente gratuit.

C’est une méthode populaire et facile d’utilisation. Ce modèle doit être utilisé pour des ventes sans tendances ni saisonnalité. Il permet de calculer des prévisions pour une période dans le futur (il faut alimenter le modèle au fur et à mesure pour calculer les prévisions de chaque période).

Le principe de la moyenne mobile simple consiste à utiliser la moyenne des ventes réelles pour un certain nombre de périodes antérieures dans le but de prévoir les ventes d’une période dans le futur.

Seul un certain nombre de données sont utilisées pour calculer la moyenne, soit les plus récentes. On utilise toujours le même nombre de données pour calculer la MMS (on détermine le nombre de données « n » avant de débuter).

Concrètement, la formule utilisée pour calculer la moyenne mobile simple est la suivante :

Où n = nombre de données utiliser pour calculer la moyenne, i = première période considérer dans le calcul de la MMS et t = dernière période utiliser dans le calcul de la MMS.

 

On utilise un « n » petit lorsque la demande fluctue beaucoup et «grand lorsque la demande est stable et fluctue de façon plutôt aléatoire.

Voici maintenant à quoi ressemble cette technique lorsqu’utilisé avec notre outil gratuit!

 

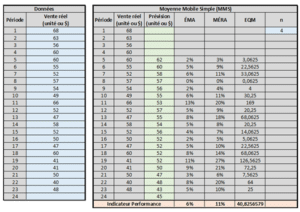
Moyenne Mobile Simple – Outil Excel

 

Pour toutes les méthodes, le principe reste le même. Entrer vos données dans les cases bleutées et les prévisions, ainsi que les indicateurs de performances se calculeront automatiquement.

Les prévisions se trouvent dans les cases vertes et les indicateurs de performances dans les cases beiges. Certaines cases ont des commentaires en guise de rappel. Par exemple, à quoi correspond les acronymes des indicateurs de performances et comment les interpréter.

Finalement, pour la moyenne mobile simple, le fichier offre la possibilité d’utiliser un « n » égal à 4, 5 ou 6.

 

 

Moyenne Mobile Pondérée (MMP)

 

La moyenne mobile pondérée est similaire à la moyenne mobile simple, mais cette fois-ci on accorde une importance (pondération) à chaque valeur utilisée pour calculer la moyenne.

Lorsqu’on utilise la moyenne mobile simple avec disons n = 4, chaque valeur équivaut à 25% du résultat final. La MMP permet de modifier cette pondération, pour par exemple, donner plus d’importance aux valeurs plus récentes.

La formule permettant de calculer les moyennes mobiles pondérées est :

Où M_i = moyenne mobile pondérée pour la période i, n = nombre de périodes utilisées pour le calcul de MMP, X_i-L = vente réelle pour une période précédente et a_L = poids ou pondération d’une valeur dans le calcul de moyenne.

Note : La somme des a_L doit être égale à 1 (ou 100%).

 

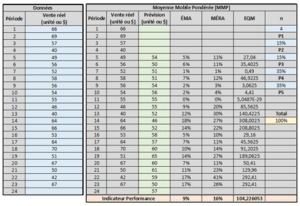
Moyenne Mobile Pondérée – Outil Excel

 

 

1. Commencer par entrer les données dans le tableau « Données » en bleu.
2. Sélectionner le « n » qui vous convient en haut à droite du tableau intitulé « Moyenne Mobile Pondérée (MMP) ». Vous avez le choix entre n égal à 3, 4 ou 5.
3. Dans les cases « P1 » à « P5 », entrer la pondération de chacune des valeurs. P1 étant la pondération de la valeur la plus vieille et P5 la plus récente. Dépendant si vous sélectionnez « n » égale à 3, 4 ou 5, il vous faudra remplir les cases « P1 » à « P3 », « P4 » ou « P5 ». La somme des pondérations doit être de 100%. La case « Total » en jaune donne la somme des pondérations. Elle affichera « Attention » si la somme des pondérations est différente de 100%.
4. Les cases vertes montrent les prévisions de ventes pour ce modèle.
5. Les cases beiges « Indicateur Performance » montrent la précision de la méthode. Elles permettent de comparer les différentes méthodes en 1 coup d’œil.

Note : En remplissant les cases « Données », toutes les méthodes d’un onglet ce calcul. Par exemple, toutes les méthodes de prévisions de vente pour une demande sans tendance ni saisonnalité vont se calculer. On peut choisir la plus précise en consultant les indicateurs de performances.

 

Lissage Exponentiel Simple (LES)

 

Le lissage exponentiel simple est une méthode simple à utiliser et qui donne souvent de meilleurs résultats que la moyenne mobile simple. Cette méthode permet d’estimer les ventes pour une période dans le futur à la fois.

Le principe du LES est « basé sur le fait que la prévision courante correspond à la prévision précédente ajustée quelque peu ». Pour ajuster cette dernière, un facteur de pondération α (généralement situé entre 0,1 et 0,3) et l’écart entre la dernière prévision et la vente réelle sont utilisés.

Pour le lissage exponentiel simple, on utilise la formule suivante :

Où S_T = ventes estimées au temps T, α = paramètre de lissage, X_T = demande à la période T et S_T-1 = ventes estimées à la période T-1.

 

Le facteur de pondération α « détermine le niveau de lissage et la vitesse de réaction à la différence entre la prévision et la demande réelle. » (Drolet, Robitaille & Désilets, 2016).

Plus la demande est fluctuante, plus un α élevé est nécessaire pour obtenir un modèle précis. À l’inverse, une demande stable nécessite un paramètre de lissage près de 0.

 

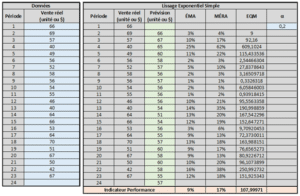
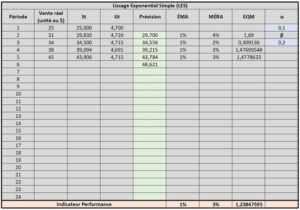
Lissage Exponentiel Simple – Outil Excel

 

 

Méthodes Prévisionnelles Avec Tendance – Prévision des Ventes

 

Régression Linéaire Simple

 

La régression linéaire simple établit une relation linéaire entre deux facteurs (variables). L’une des variables est dépendante (y) de l’autre (x, variable indépendante). La relation établie prend la forme suivante :

Y = ax + b

Les paramètres « a » et « b » représente respectivement la pente de la droite linéaire et l’ordonnée à l’origine. Cette méthode nécessite quelques données pour établir une relation linéaire précise. Pour connaître la précision de ce modèle, on utilise les coefficients de corrélation « R » et de détermination « R² ».

Voici un tableau présentant la signification de « R » en fonction de sa valeur :

 

Valeur de « R »	Signification
0,90 à 1,00 OU -1,00 à -0,90	Corrélation forte
0,70 à 0,8999 OU -0,8999 à -0,70	Bonne corrélation
0,4 à 0,6999 OU -0,6999 à -0,40	Corrélation faible à moyenne
-0,3999 à 0,3999	Mauvaise corrélation

 

Pour le coefficient de détermination, plus la valeur de « R² » se rapproche de 1, plus la relation entre x et y est bonne. Par exemple, un R² = 0,9 indique que 90% de la valeur de Y est expliqué par la variation de la variable indépendante x.

 

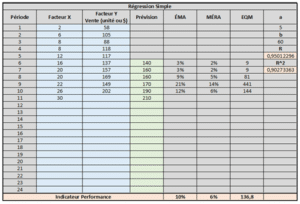
Régression Linéaire Simple – Outil Excel

 

 

Régression Linéaire Multiple

 

La régression multiple est, selon (Drolet, Robitaille & Désilets, 2016), « une extension de la régression linéaire simple permettant de prendre en considération plusieurs variables indépendantes X afin d’expliquer le comportement d’une variable dépendante Y. » On notera les variables indépendantes X₁, X₂, …, X_n.

La régression multiple suit une fonction mathématique : Y = b0 + b1X1 + b2X2 + … + BnXn

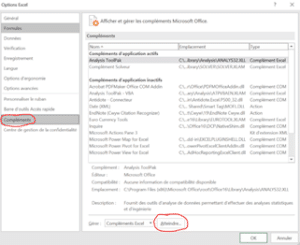
Pour avoir accès à la régression multiple sur Excel, il faut tout d’abord installer/ajouter l’utilitaire d’analyse Excel. Voici comment procéder pour l’ajouter si vous ne l’avez pas déjà fait :

 

Étape 1 : Aller dans Fichier

 

 

 

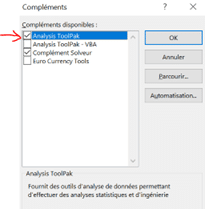
Étape 2 : Cliquer sur « Options », puis complément et finalement « Atteindre »

 

       

 

Étape 3 : Sélectionner « Utilitaire d’analyse » ou « Analysis Toolpack »

 

 

Régression Linéaire Multiple – Outil Excel

 

Pour utiliser la régression multiple avec le fichier fourni dans l’article, voici comment procéder :

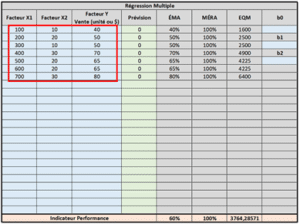
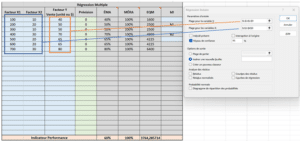
Étape 1 : Entrée vos données dans le tableau intitulé « Régression Multiple »

 

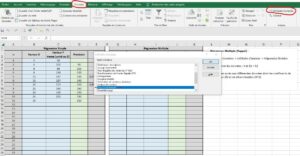
Étape 2. Lancer l’utilitaire d’analyse dans l’onglet « donnée » et sélectionner la régression linéaire

 

Étape 3 : Entrer les variables dépendantes (« X1 » et « X2 ») et la variable indépendante aux endroits montrés ci-bas.

 

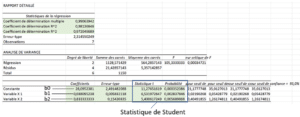
Étape 4 : Avec les résultats obtenus, on obtient les coefficients de déterminations, l’ordonnée à l’origine, les pentes de l’équation, ainsi que les statistiques de Student pour vérifier que les variables indépendantes ont bel et bien un effet sur la variable indépendante (avec un seuil de confiance de 95%).

 

Dans cet exemple, on voit que les statistiques de Student donnent une probabilité de 0,002837 pour « X1 » et 0,005689 pour « X2 ». Ces probabilités sont inférieures à 0,05, donc on peut affirmer que les variables indépendantes ont un effet sur la variable dépendante avec un seuil de confiance de 95%.

Le coefficient de détermination multiple de 0,9906… indique que le modèle explique 99% de la variation de « Y ». Ce qui est très bon. (Voir explication pour coefficient de détermination dans la section « Régression Linéaire » au besoin).

 

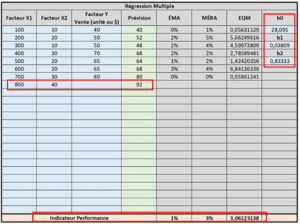
Étape 5 : Entrer les données « b0 », « b1 » et « b2 » pour générer les calculs de prévisions en fonctions de la régression multiple obtenues. Au fur et à mesure que vous avez de nouvelles données, vous pouvez répéter l’exercice afin de mettre le modèle à jour (recalculer b0, b1, b2). Entrer des données dans X1 et X2 pour générer des prévisions.

 

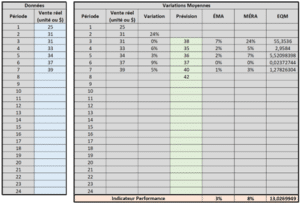
Variation Moyenne

 

La méthode des variations moyennes est une méthode avec une précision généralement faible à moyenne. C’est une méthode simple et rapide à utiliser. Elle nécessite peu de données pour établir des précisions.

Pour utiliser cette méthode, on calcule la variation moyenne des ventes pour calculer les prévisions des prochaines périodes. Voici les formules utilisées :

 

Variation =

 

Accroissement moyen =

 

Prévision de la période (i+1) = Vente réelle période i * (100% + accroissement moyen)

 

Variation Moyenne – Outil Excel

 

 

Moyenne Mobile Double (MMD)

 

La moyenne mobile double permet d’établir des prévisions de ventes avec une précision moyenne à bonne. Cette méthode est utilisée pour des ventes avec une tendance à la hausse (ou la baisse), mais sans saisonnalité.

La MMD consiste à effectuer deux moyennes mobiles pour calculer une prévision, versus une avec la moyenne mobile simple.

Formule mathématique :

Prévision I+i (T) =

Où M_I = Moyenne mobile à la période I, M_I^[2] = Moyenne mobile double à la période I, t = nombre de période dans le futur et n = nombre de périodes utilisées pour le calcul de moyenne mobile simple et double.

 

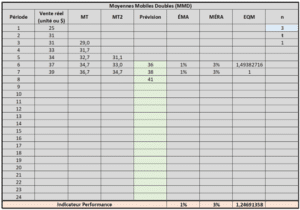
Moyenne Mobile Double (MMD) – Outil Excel 

 

 

Pour cette méthode, vous pouvez sélectionner un « n » égale à 3, 4, 5 ou 6 pour effectuer les calculs de moyennes mobiles. Cela permet d’obtenir une meilleure précision et de réaliser plus ou moins de prévisions avec le même nombre de données.

Par exemple, avec n =6, il faut minimalement 11 données avant d’obtenir 1 prévision. Avec un « n » = 3, on a besoin de seulement 5 données. Toutefois, la précision des données varie entre n = 3 et n =6. Dépendant des ventes, il est bien de tester différent n pour obtenir la meilleure précision possible.

 

Lissage Exponentiel Simple Avec Tendance

 

Le lissage exponentiel simple est un modèle qui donne souvent de bons résultats. Lorsqu’il y a une tendance dans les ventes, il faut ajouter un facteur de tendance linéaire et une constante de lissage pour la tendance linéaire.

Les formules utilisées et automatisées dans le fichier Excel pour cette technique sont les suivantes :

Y_t = αV_t + (1- α)(P_t-1 + G_t-1)

Avec G_t = β(Y_t – Y_t-1)+(1-β)G_t-1

Et P_t+1 = Y_T + G_T

Où Y_t = Ventes estimées et lissées au temps t, V_t = Ventes actuelles au temps t, G_t = facteur de tendance linéaire lissé, α = constante de lissage pour variation aléatoire, β = constante de lissage pour la tendance linéaire et P_T = prévision pour la période t.

Généralement : 0,1 < α < 0,3 et 0,05 < β < 0,2

 

Lissage Exponentiel Simple Avec Tendance – Outil Excel

 

 

Entrée vos données dans le tableau intitulé « Données » et sélectionner entrée les paramètres α et β dans les cases bleutées. Essayer différentes valeurs et conserver celle qui convient le mieux à votre situation. Fiez-vous aux indicateurs de performance pour faire votre choix!

 

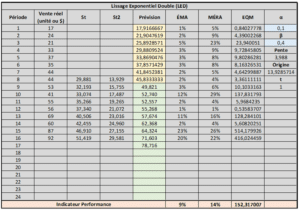
Lissage Exponentiel Double (LED)

 

Le lissage exponentiel double permet aussi d’obtenir de bonne prévision. C’est l’un des modèles à surveiller, car il y a de bonnes chances qu’il ait les meilleurs indicateurs de performance pour vous (c’est-à-dire que les écarts moyens entre les prévisions et les ventes réelles sont faibles).

Voici la procédure pour effectuer du LED. Cette méthode est déjà programmée dans notre fichier gratuit, alors vous pouvez sauter cette section si vous le souhaitez. Pour les intéresser :

Posons : X : Variable indépendante (période) ; Y : Variable dépendante (vente)

1. Pour commencer, il faut calculer les estimer initiaux en utilisant la régression linéaire. Pour obtenir une précision acceptable, il est recommandé d’utiliser minimalement 8 données.

S₀ = P₀ – ((β/α) * a) et S₀(2) = P₀ – (2 * (β/α) * b)

Où (dans le cas où on utilise 8 données pour faire la régression linéaire) S₀ = S₈, S₀(2) = S₈(2), P₀ = P₈ = Prévision de la 8^e période (calculer avec la régression)

2. Une fois les estimations initiales calculées, on peut procéder aux prévisions par lissage exponentiel double.

P_0+t = P_8+t = (( 2 + (αt / β)) * S₈) – (( 1 + (αt / β)) * S₈(2))

S_0+t = α * X_t + (1 – α)*S_0+t-1 et S_0+t(2) = α * S_0+t + (1 – α)*S_0+t-1(2)

 

Lissage Exponentiel Double – Outil Excel

 

 

Essayer des valeurs de α et β pour obtenir le meilleur modèle selon votre situation.

0 < α < 1 et 0 < β < 1

 

Méthodes Prévisionnelles Avec Saisonnalité – Prévision des Ventes

 

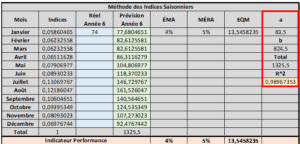
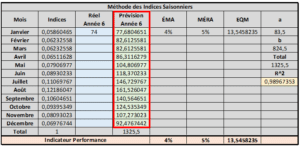
Prévisions Saisonnières à l’aide d’Indice

 

Cette première méthode de prévision de vente avec saisonnalité n’utilise pas la « désaisonnalisation » pour effectuer les calculs de prévisions. C’est plutôt avec l’aide d’indice saisonnier que les prévisions se calculent. La méthode est simple et efficace.

Pour montrer le principe, utilisons le fichier Excel fourni dans l’article.

 

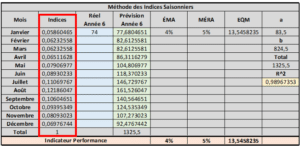
Prévisions Saisonnières à l’aide d’Indice – Outil Excel

 

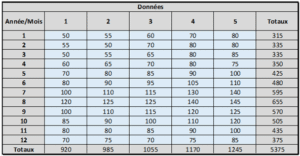
Étape 1 : Entrée vos données de ventes passées et calculer la somme des lignes et des colonnes

 

 

Étape 2 : Calculer les indices saisonniers. Pour ce faire, diviser la somme d’un mois par le total des ventes. Par exemple, l’indice de Janvier se calcule de la façon suivante :

315 / 5375 = 0,05860…

Le total des indices doit être égal à 1.

 

 

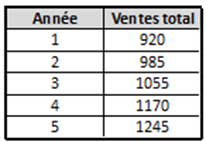
Étape 3 : Ensuite, effectuer la régression linéaire avec les données totales des années.

 

 

Y = aX + b = 83,5X + 824,5

 

 

Étape 4 : Maintenant, pour effectuer les prévisions, utiliser la régression linéaire et les indices saisonniers.

Par exemple, pour janvier de la 6^e année, la prévision sera de :

Y = 83,5*6 + 824,5 = 1325,5

1325,5 * 0,05860465 = 77,68…

 

 

Autres Méthodes Pour Ventes Saisonnières

 

Il existe d’autres modèles pour les ventes saisonnières dont le modèle de Winters qui offre une bonne précision, mais qui est plus complexe que les autres modèles et les méthodes par désaisonnalisation.

Pour plus d’information par rapport à ces méthodes, contactez-nous.

 

 

Conclusion

 

Les prévisions de ventes sont une pierre angulaire pour les entreprises, car de celles-ci découlent les budgets prévisionnels, une gestion des stocks optimale, etc. Cela peut même permettre de faciliter les demandes de financement.

Dans cet article, une multitude de méthodes prévisionnelle sont présentées et programmées dans un fichier Excel. Les méthodes sont séparées en fonction du contexte de vente de l’entreprise (par niveau ou stable, avec tendance ou avec saisonnalité).

Finalement, les différents indicateurs de performance permettant de comparer les méthodes et identifier les meilleurs selon notre situation sont présentés. De plus, celles-ci sont aussi programmées dans le chiffrier Excel afin de comparer les méthodes en un simple coup d’œil!

 

Référence : 

Drolet, J., Robitaille, J. & Désilets, B. (2016). Méthodes Prévisionnelles Partie 1, UQTR, PDF.

Drolet, J., Robitaille, J. & Désilets, B. (2016). Méthodes Prévisionnelles Partie 2, UQTR, PDF.

Désilets, B. (2016). Partie 3 Notes de cours sur les méthode prévisionnelles avec saisonnalité, UQTR, PDF.